Nous n’allons pas parler cette fois de la fameuse fonction Zeta mais des sphères de Riemann qui me fascinent tout autant et depuis longtemps. Cela tient sans doute à l’histoire de Bernard Riemann lui même, mathématicien génial s’il en était… Il souffrait de « dépressions nerveuses », incurables à l’époque, comme Cantor, et comme tant d’autres de ces puissants esprits dont certains finirent « fous »…

D’ailleurs, tandis qu’il mourrait de la tuberculose en Italie, sa femme de ménage jetait quelques-uns des papiers en désordre dans son bureau à Göttingen, y compris beaucoup de travail inédit. Riemann refusait en effet de publier du travail qu’il jugeait incomplet et certaines de ses idées profondes ont sans doute été perdues à jamais…

Fractale de Riemann

Naturellement, la formule a été adaptée pour un usage fractal dans Mandelbulb3D même si son emploi ralentit considérablement les rendus des combinaisons le contenant. Mais c’est ce qui donne cet inimitable aspect « encagé », avec  toutes ces portes donnant sur l’infini…

Mais pour voir vraiment à quoi çà ressemble, n’hésitez pas à plonger à l’intérieur et profond : la sphère fractale est en effet pleine de trous ! (Musique Eric Le Guen).

 

Il y a quelques années, une brève exploration m’avait amené dans ce sanctuaire à bateau, ces épaves oubliées au coeur de la sphère complexe et m’ayant inspiré ce tableau intitulé, forcément, « Riemann’s wreck »…

Pour illustrer ce billet, je me suis depuis aventuré dans une des cavités latérales, gouffre infini comme il se doit, le temps de découvrir un point de vue intéressant. Fibre de carbone glacée sur une lointaine planète ? Alliage biomécanique de quelque vaisseau extraterrestre ? Notre explorateur nous en dira plus au bas de ce rappel…

Naturellement, j’ai cherché à calculer cette sphère de Riemann sous forme de « solide » 3D. Ne pouvant hélas dépasser dans Mandelbulb3D une définition de 256 pixels au cube (au delà ma machine explose, j’ai essayé…)
Pas étonnant donc que j’obtienne ces sphérules mal définies (quelques millions de faces, tout de même) qui, avec la texture dorée idoine, constituent tout de même de fort honorables pépites…

Vers Riemann 2 et au delà…

Bien évidemment, la sphère de Riemann ne pouvait suffire aux psychopathes fractalistes qui en ont programmés plusieurs variations. Dans Mandelbulb3D l’une d’elles, nommée tout simplement Riemann 2 est basée sur une équation d’un certain « MslToe » (lourds, lourds les fractalistes scientifiques, cachés derrière leurs pseudos)…

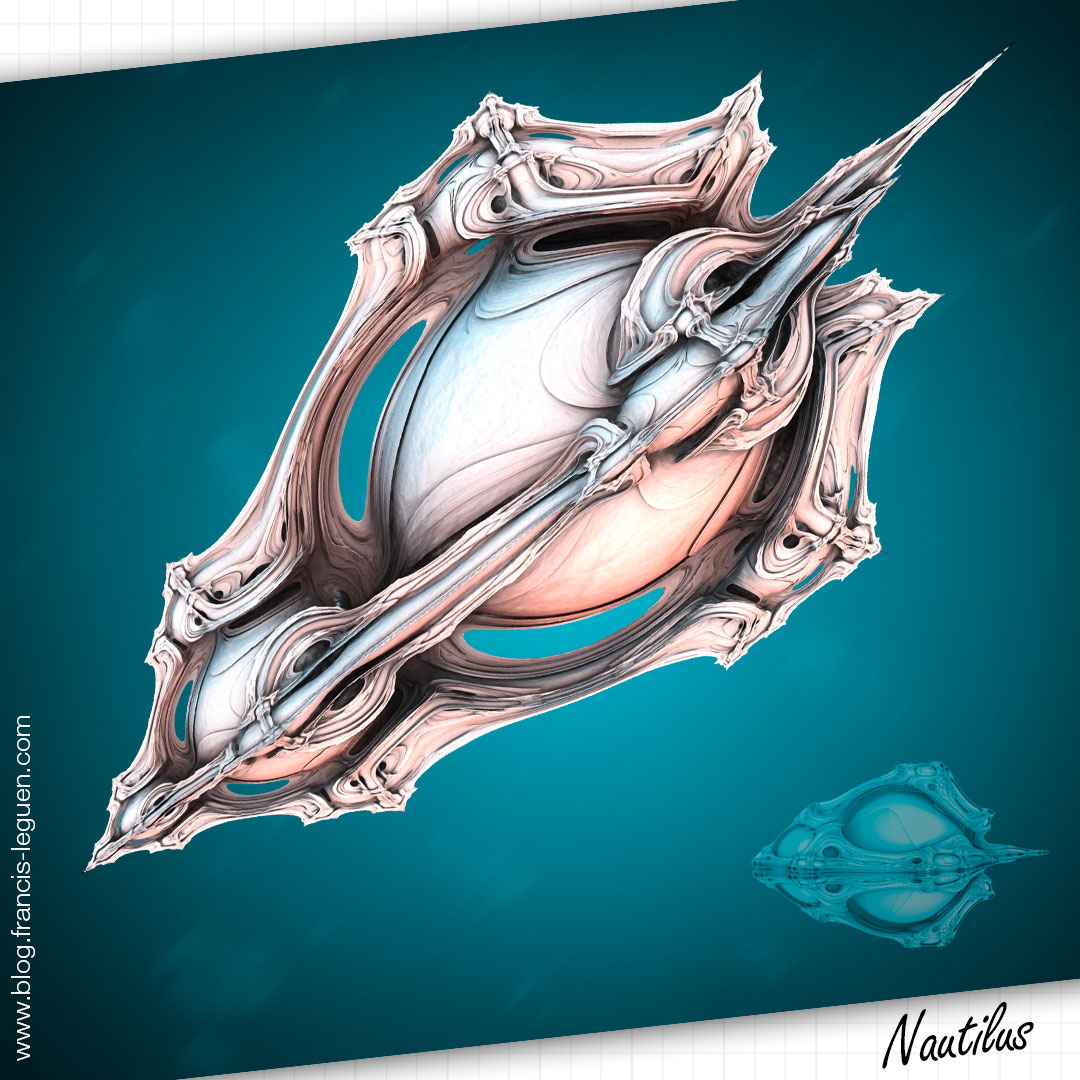
Son exploration rapide me menait à cette étrange maquette de « Nautilus » ci-dessus et, en jouant sur la « rotation en Z », à des choux « Romanexquis » potentiels…

 

 

C’est alors que je m’aperçu que les sphères de Riemann étaient aussi implantées dans Mandelbulber avec au programme 4 variations de celles-ci. Et toujours l’énigmatique « MslToe »…

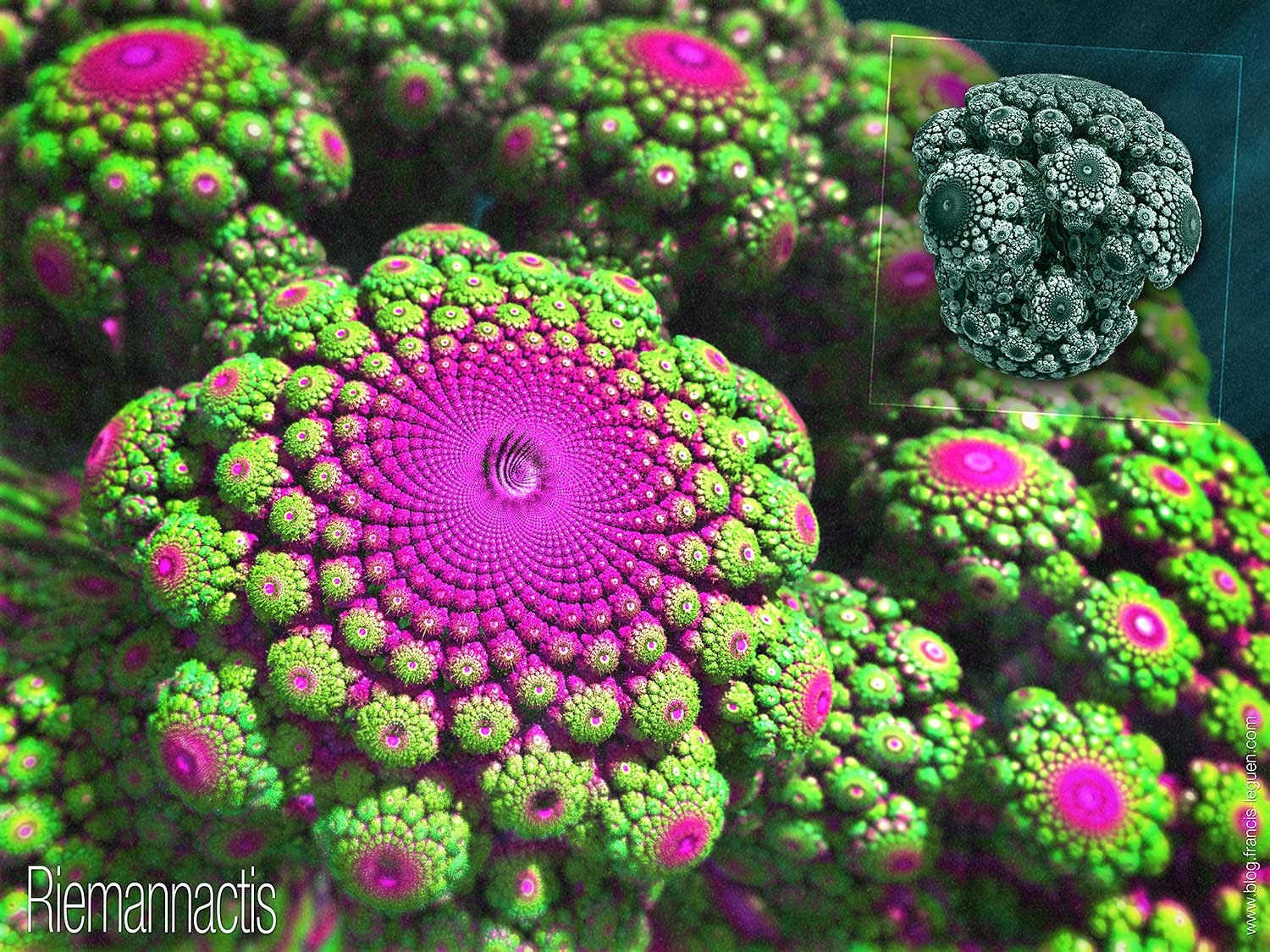
Changement de logiciel, donc, et sur la base de la « Riemann sphere Msltoe V1 » et en utilisant la charte de couleur des anémones corynactis (vert fluo et rose tyrien) je parvenais à générer ces créatures marines filtrantes ci-dessous. Si.

 

 

 

 

Les JIT du bocal

Il y aurait déjà eu largement de quoi faire avec ces quelques formules à l’échelle de l’infini mais il a fallu qu’un autre illuminé (Gannjondal) accouche d’une kyrielle d’autres formules pour Mandelbulb3D, des équations « non officielles » regroupées sous le sobriquet de « JIT formulas » qui ne sont pas implémentées en standard dans le logiciel et qu’il faut aller chercher et installer par soi même « sans garantie ». D’ailleurs, peu après ces hasardeuses manœuvres, mon Mac entrait en éruption. Bilan : deux barrettes mémoires dans la sciure… RIP. Nan, JIT…

Mais ces formules valent le détour, permettant de générer d’incroyables formes au prix de minuscules variations de paramètres. Les effets les plus intéressants sont obtenus en les combinant avec d’autres formules « classiques », en l’occurence, « Integer Power » ou « Menger 3 ». Pensez à explorer également les variations Julia.

Voici donc quelques photos volées (tant qu’on est dans les choux) au cours de l’exploration qui terminent ce tour d’horizon des différentes fractales de Riemann.